Изучение эпидемических проявлений инфекционных болезней – одна из ведущих областей эпидемиологических исследований. Наблюдения за антигенной изменчивостью возбудителя и инфекционной заболеваемостью в коллективах закрытого типа дают наиболее четкую картину развития процесса. Результаты исследований такого рода позволили В.Д. Белякову выявить ряд закономерностей и обобщить их в концепцию саморегуляции эпидемического процесса [1, 2]. В основе этой концепции – рассмотрение «изменений уровня заболеваемости как проявления внутренних законов развития эпидемического процесса, где вирулентность … и восприимчивость … представляют единое явление» [3: 150]. Эта концепция, нынче редко вспоминаемая, закладывает основу системно-динамического подхода к анализу процессов взаимодействия популяций возбудителя и хозяина. Ее ценность – в фундаментальности представлений о природе эпидемического процесса. Чтобы дать этой концепции дальнейшую жизнь, необходимо найти дальнейшее направление ее развития. Таким направлением может стать системно-динамическое освещение тех фактов, которые были обнаружены в эксперименте, но не получили такого освещения. Речь идет о механизме взаимосвязи фазовых преобразований двух популяций, то есть о конкретных регуляторных связях между фазовыми состояниями и интенсивностями межфазовых переходов. Смена фазовых состояний взаимодействующих популяций должна найти выражение в понятной компартментной модели, дополненной внутренними регуляторными связями. При этом фазовый сдвиг между пиками вирулентности и заболеваемости, обнаруженный в эксперименте [1] и отмеченный как факт наличия внутренней регуляции, должен органически вписаться в картину совместных фазовых преобразований двух популяций. Подобную картину приводят В.Д. Беляков и соавт. [2]. Однако она лишь подсказывает возможные связи, но не определяет их явно. Задача данной статьи – предложить конкретную схему взаимосвязей фазовых преобразований двух популяций и показать адекватность модели, построенной в соответствии с этой схемой.

Материалы и методы

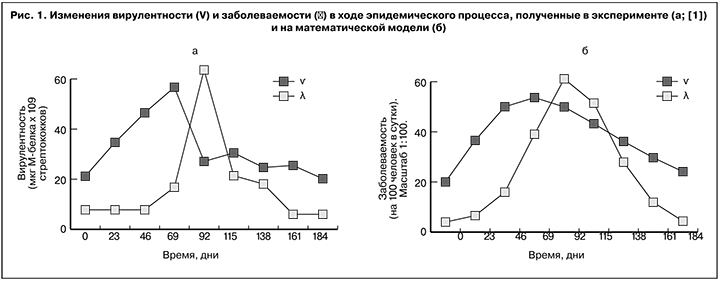
В качестве материала взяты данные наблюдений, полученные А.П. Ходыревым (в интерпретации Белякова) по развитию эпидемического процесса стрептококковой инфекции в группе учащихся [1]. В процессе наблюдений измеряли уровень заболеваемости ангиной (на 100 человек в сутки) и вирулентность стрептококков (по содержанию М-белка в мкг х109 стрептококков). Графики изменения заболеваемости и вирулентности, построенные по этим данным, показаны на рис.1.

В качестве метода исследования выбрано математическое моделирование, позволяющее проверять различные предположения относительно строения внутренней регуляции путем перебора разных комбинаций регуляторных связей. В данном случае это связи между фазовыми преобразованиями двух популяций. Если введенные регуляторные связи позволяют воспроизвести картину наблюдаемого явления, то адекватность модели, содержащей эти связи, может считаться установленной. Приведем описание модели.

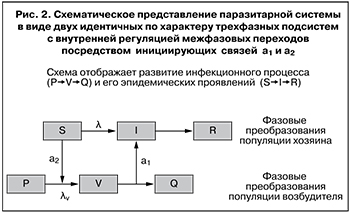
Модель. Будем полагать, что влияние инфекционного процесса на эпидемический состоит в изменении состава популяции хозяина, а обратное влияние эпидемического процесса на инфекционный – в изменении состава популяции возбудителя. Эти изменения количественно выражаются через доли участвующих компонент. Обозначим через P долю авирулентных стрептококков, через V – долю вирулентных и через Q – долю потерявших вирулентность. Тогда последовательность переходов P→V→Q отобразит фазовые преобразования популяции возбудителя. Для отображения фазовых преобразований популяции хозяина воспользуемся известной моделью SIR, где S – доля восприимчивых, I – инфицированных, R – иммунных. Две последовательности переходов, P→V→Q и S→I→ R, свяжем регуляторными зависимостями. Обозначим через λv интенсивность перехода P→V, приняв λv = a2PV), а через λ – интенсивность перехода S→I (λ = a1SI) и введем предположение о взаимной инициации этих переходов, то есть о наличии регуляторных зависимостей λv от S и λ от V (рис. 2). Первая связь отражает необходимость наличия восприимчивых для инициации инфекционного процесса, вторая – необходимость наличия вирулентного возбудителя для инициации эпидемического процесса. Предположение о взаимной инициации этих двух процессов является дополнением к концепции саморегуляции эпидемического процесса. Математическая модель, построенная в соответствии с этим дополнением, имеет вид: dS/dt = – a1SI, dI/dt = a1SI – b1I, dR/dt = b1I, a1 = k1V, dP/dt = – a2PV, dV/dt = a2PV – b2V, dQ/dt = b2V, a2 = k2S.

Результаты и обсуждение

Численная идентификация математической модели проводилась по временному сдвигу между пиками заболеваемости и вирулентности и их величинам. При сравнения рисунков 1а и 1б видно, что идентифицированная модель качественно верно воспроизводит характер динамики показателей заболеваемости (λ) и вирулентности (V): пик вирулентности опережает пик заболеваемости, а промежуток между ними близок к реальному, причем высоты пиков соответствуют опытным (более гладкий вид кривых – результат модельной идеализации). Следовательно, введенные регуляторные связи могут считаться отвечающими действительности. В этом случае предположение о взаимной инициации фазовых преобразований двух популяций можно считать непротиворечащим действительности. Тем самым обращение к системному анализу дало основание расширить представление об эпидемических проявлениях инфекционного процесса, а именно построить инфекционно-эпидемическую модель, связав два уровня иерархии биологических процессов в одно целое и дополнив положение о ведущей роли возбудителя не менее важной ответной ролью хозяина. При этом попытка дать системно-динамическое объяснение фазовому сдвигу привела к мысли о необходимости взаимной инициации двух разноуровневых процессов. В результате взаимодействие популяций хозяина и возбудителя получило искомое схематическое представление, показанное на рис. 2. Согласно этому представлению, начальное фазовое состояние популяции хозяина (S) создает условия для начала фазовых изменений популяции возбудителя – активизирует переход его в вирулентное состояние (V), а вирулентное состояние популяции возбудителя вызывает фазовое изменение популяции хозяина – переход его в инфицированное состояние (I).

Отметим, что начальная стадия P фазовых преобразований популяции возбудителя ответственна за наличие стрептококков, способных синтезировать M-белок. Как предвирулентная стадия микробиологического процесса она характерна заметно бóльшим начальным превышением доли таких стрептококков над долей вирулентных. Введение этого состояния позволило получить требуемый фазовый сдвиг и этим наглядно воспроизвести опережение фазовых изменений популяции возбудителя. Факт опережения отоб­ражается на рис. 2 сдвигом цепочки фазовых превращений популяции хозяина вправо относительно такой же цепочки для возбудителя. Схема взаимодействия популяций возбудителя и хозяина приобретает вид замкнутой цепи, характерный для саморегулируемых процессов, что на рис. 2 отображено цепочкой S, a2, V, a1. Задействование прочих фаз требует введения дополнительных предположений относительно их влияния на процесс взаимодействия популяций возбудителя и хозяина.

Более детальное исследование поведения модели позволило обнаружить следующую особенность: при наличии выраженной чувствительности пика заболеваемости к изменению регуляторных коэффициентов k2, m2 отмечается весьма слабая чувствительность пика вирулентности к изменению обоих коэффициентов. Этот факт свидетельствует о наличии относительной автономии фазовых преобразований популяции возбудителя, хотя и протекающих в среде восприимчивых представителей хозяина. Вступая в отношения с восприимчивым хозяином, возбудитель способен наращивать свою вирулентность, раз за разом меняя хозяина. Это свойство возбудителя (и как способ восстановления прочих свойств) в равной степени относится и к популяции стрептококков: «Пассаж возбудителя через восприимчивые особи приводит к … повышению вирулентности …» [4: 132]. Необходимость в связывании с хозяином составляет смысловое содержание регуляторного коэффициента m2. Незначительное его изменение влечет значительное изменение в силе процесса, тогда как значительные изменения числа восприимчивых сказываются меньше из-за череды смен хозяина. Можно сказать, что уменьшение числа восприимчивых компенсируется увеличением частоты их смен. Данное объяснение лишь иначе интерпретирует факт, отмеченный В.Д. Беляковым и соавт. [2] как изменение числа восприимчивых в цепочке передач возбудителя. Более детальное моделирование этого процесса позволило бы получить более полное понимание его природы.

Предложенная модель далеко не в полной мере отражает разнообразные формы проявления стрептококковой инфекции, в частности, скрытые формы, представляющие эпидемическую опасность [5]. Так как в модели не выделена группа носителей, то невозможно проследить переход носительства в манифестную форму. Хотя в опытах Белякова–Ходырева и велся подсчет числа носителей, но не прослеживалась доля заболевающих среди них. В этом отношении более полезны данные А.А. Яковлева [6], где наблюдение этой доли прослеживалось во времени и отмечался лаг в переходе носительства в манифестную форму. Наличие лага подтверждают и И.В. Фельдблюм и соавт. [7]. Так как бессимптомные формы носительства чрезвычайно распространены, создание математической модели развития стрептококковых инфекций с учетом носительства было бы весьма полезно, особенно в части изучения механизма перехода в манифестную форму (подобная попытка была предпринята И.Д. Колесиным и соавт. для гриппа [8]).

Однако даже имеющаяся модель может соориентировать в вопросе о роли носителей, если раскрыть природу коэффициента m1 через их число (обозначив его через Ip ): m1 = µ1Ip. Как показывает численный эксперимент, отсутствие бессимптомных носителей в неиммунном малом коллективе, что имитируется заданием Ip = 0, существенно сдерживает развитие эпидемической вспышки, однако в большом коллективе, где имеются условия для формирования эпидемического варианта возбудителя, их отсутствие почти не сказывается на развитии эпидемии. Следовательно, в случае малого коллектива наличие носителей с выделением возбудителя во внешнюю среду является определяющим, а для большого коллектива этот фактор менее важен. Переменный коэффициент m1 лишь подсказывает возможную реакцию процесса на изменение фактора Ip. Для более детального изучения его влияния требуется расширение модели путем введения дополнительной переменной Ip.

Подобный же подход к разрешению вопроса о роли носителей можно применить и к коэффициенту m2, раскрывая его природу через долю «дремлющих» стрептококков (PL): m2 = µ2PL. Численный эксперимент показывает, что увеличение их доли при достаточно большом числе восприимчивых может вызвать эпидемию, а при малом – лишь поддерживать инфекцию, протекающую в этом случае без выделения возбудителя, но с продукцией антител. Действительно, В.Д. Беляков и соавт. выделили случаи, при которых «наличие типоспецифических антител в крови сочетается с носительством стрептококков в течение месяцев и даже лет» [4: 46]. Введение в модель показателя титра антител позволило бы детальнее изучить этот факт и осветить ряд других, связанных с ним.

Изучение скрыто протекающего эпидемичес­кого процесса представляет особый интерес ввиду малоизученности этой формы. Это не является исключением и для стрептококков [7]. Скрытая форма инфекции (носительствo без выделения возбудителя во внешнюю среду) не позволяет своевременно обнаруживать лиц с бессимптомным течением инфекции. Согласно результатам исследования А.А. Яковлева [6], такая инфекция может перейти в манифестную форму при наличии стресса. Было бы интересно ввести в модель дополнительный фактор, имитирующий стресс, и проверить наличие «порога» чувствительности, с переходом через который Ip переходит в I. Это, однако, требует усложнения модели и наличия данных для ее идентификации, что, в свою очередь, связано с дорогостоящим экспериментом.

Выполненное исследование показало необходимость сочетания концепции саморегуляции эпидемического процесса с положением о взаимной инициации фазовых преобразований двух популяций. Это расширение концепции стало возможным только в силу системно-динамического подхода, предпринятого для объяснения фазового сдвига. В ходе исследования показана адекватность системно-динамической модели, связывающей эпидемические проявления инфекционного процесса с фазовыми преобразованиями популяций, и отмечена слабая чувствительность инфекционного уровня к изменениям на эпидемическом уровне. Это обстоятельство дало повод говорить об относительной автономии инфекционного процесса. Дополнительно показана определяющая роль бессимптомного носительства для эпидемической вспышки в малом неиммунном коллективе и незначительная роль – в большом.